知識點總結
一.二次函數的最值：
1.如果自變量的取值是全體實數，那么二次函數在圖象頂點處取到最大值(或最小值)。
這時有兩種方法求最值：一種是利用頂點坐標公式，一種是利用配方計算。
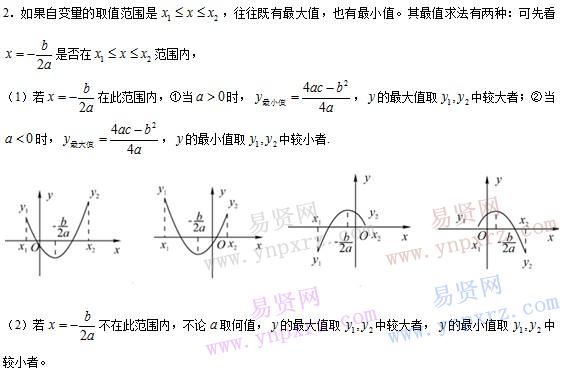
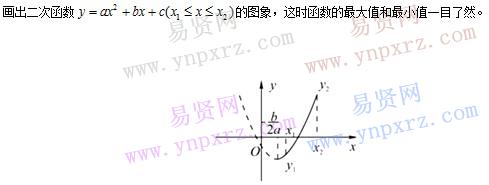
二.二次函數與一元二次方程、二次三項式的關系
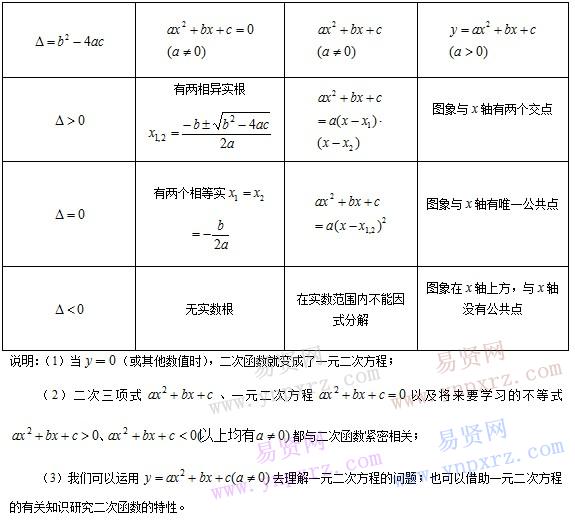
三.二次函數的實際應用
在公路、橋梁、隧道、城市建設等很多方面都有拋物線型;生產和生活中，有很多“利潤最大”、“用料最少”、“開支最節約”、“線路最短”、“面積最大”等問題，它們都有可能用到二次函數關系，用到二次函數的最值。
那么解決這類問題的一般步驟是：
第一步：設自變量;
第二步：建立函數解析式;
第三步：確定自變量取值范圍;
第四步：根據頂點坐標公式或配方法求出最值(在自變量的取值范圍內)。
常見考法
(1)考查一些帶約束條件的二次函數最值;
(2)結合二次函數考查一些創新問題。
誤區提醒
(1)忽略自變量的取值范圍，所求最值不符合實際意義;
(2)二次函數的坐標系建立的不恰當，給解題帶來了困難。
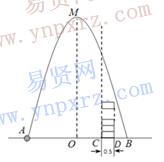
【典型例題】(2010 四川南充)如圖，在水平地面點A處有一網球發射器向空中發射網球，網球飛行路線是一條拋物線，在地面上落點為B.有人在直線AB上點C(靠點B一側)豎直向上擺放無蓋的圓柱形桶，試圖讓網球落入桶內.已知AB=4米，AC=3米，網球飛行最大高度OM=5米，圓柱形桶的直徑為0.5米，高為0.3米(網球的體積和圓柱形桶的厚度忽略不計).
(1)如果豎直擺放5個圓柱形桶時，網球能不能落入桶內?
(2)當豎直擺放圓柱形桶多少個時，網球可以落入桶內?
公眾號
事業單位
當前位置：
公考類
招聘類
各類考試
