等量代換思路
有些題的數量關系十分隱蔽,如果用一般的分析推理,難于找出數量之間的內在聯系,求出要求的數量。那么我們就根據已知條件與未知條件相等的關系,使未知條件轉化為已知條件,使隱蔽的數量關系明朗化,促使問題迎刃而解。這種思路叫等量代換思路。
例1 如圖2.15的正方形邊長是6厘米,甲三角形是正方形中的一部分,乙三角形的面積比甲三角形大6平方厘米,求CE長多少厘米?
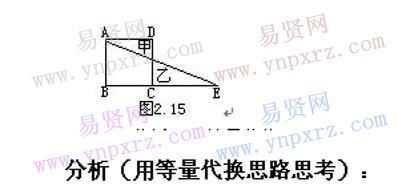
分析(用等量代換思路思考):
按一般思路,要求CE的長,必須知道乙三角形的面積和高,而這兩個條件都不知道,似乎無法入手。用等量代換思路,我們可以求出三角形ABE的面積,從而求出CE的長,怎樣求這個三角形的面積呢?設梯形為丙:
已知 乙=甲+6
丙+甲=6×6=36
用甲+6代換乙,可得丙+乙=丙+甲+6=36+6=42
即三角形ABE的面積等于42平方厘米,這樣,再來求CE的長就簡單了。
例2 有三堆棋子,每堆棋子數一樣多,并且都只有黑白兩色棋子。第一
這三堆棋子集中一起,問白子占全部棋子的幾分之幾?
分析(用等量代換的思路來探討):
這道題數量關系比較復雜,如果我們把第一堆里的黑子和第二堆的白子對換一下,那么這個問題就簡單多了。出現了下面這個等式。
第一堆(全部是白子)=第二堆(全部是黑子)
=第三堆(白子+黑子) (這里指的棋子數)
份,則第二堆(全部黑子)為3份,這樣就出現了每堆棋子為3份,3堆棋子的總份數自然就出來了。而第三堆黑子占了2份,白子自然就只有3—2=1份了。第一堆換成了全部白子,所以白子總共是幾份也可求出。最后去解決白子占全部棋子的幾分之幾就非常容易了。